In this tutorial you will learn about PID functionality, as well as how it is used in Industrial Control environments.
P= Proportional
I= Integral
D= Derivative
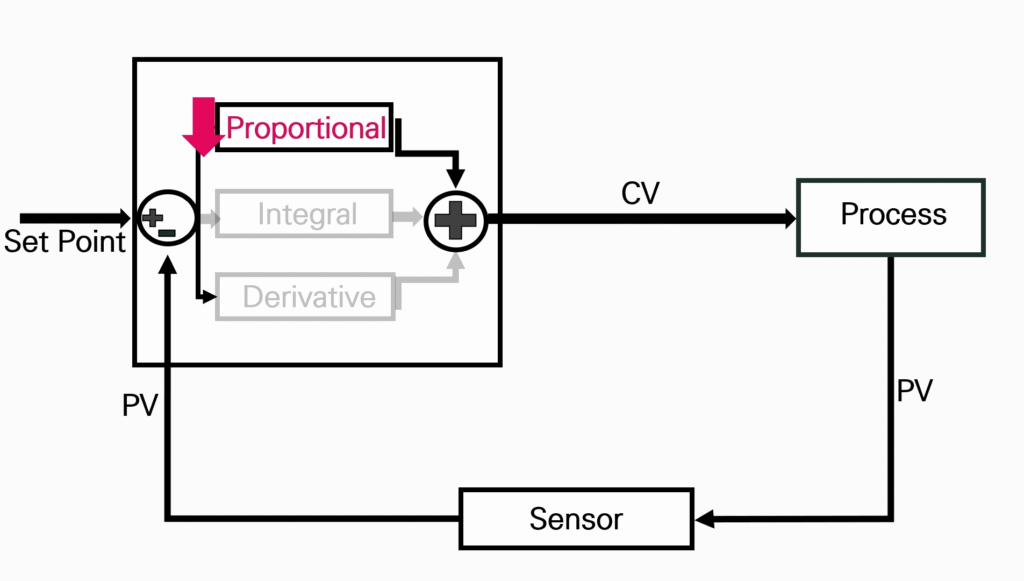
The basic idea of a PID controller is to read a sensor, then compute the desired actuator output by calculating proportional, integral and derivative responses and summing those three components to compute the output.
PID control is a control loop feedback mechanism in which the controller continuously calculates an “error value” as the difference between a measured process variable and a desired set point (target value).
This Proportional, Integral and Derivative controller attempts to minimize the error over time by adjusting a control variable to a new value.
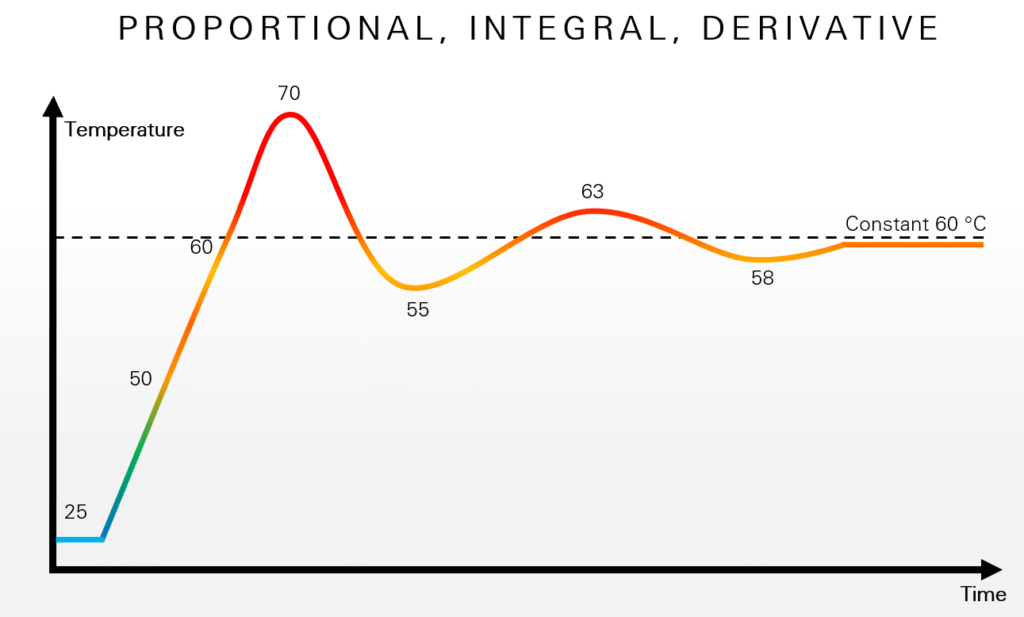
A PID is used by control engineers to regulate temperature, flow, pressure, speed and other process variables in industrial control systems.
A PID can be used to keep something constant.
Temperature would be a prime example of this:
Proportional
This can be called Proportional Gain or Proportional Band.
Proportional is usually abbreviated as Kp.
It accounts for present values of the error.
Proportional determines how fast the system responds. Adjusting this properly will result in less oscillation when headed towards the target value.
Integral
This can be called the “Reset”.
Integral is often abbreviated as Ki or Ti.
It determines how fast the “error” is removed and accounts for past values of the “error”.
It cuts down the error caused by Proportional Gain.
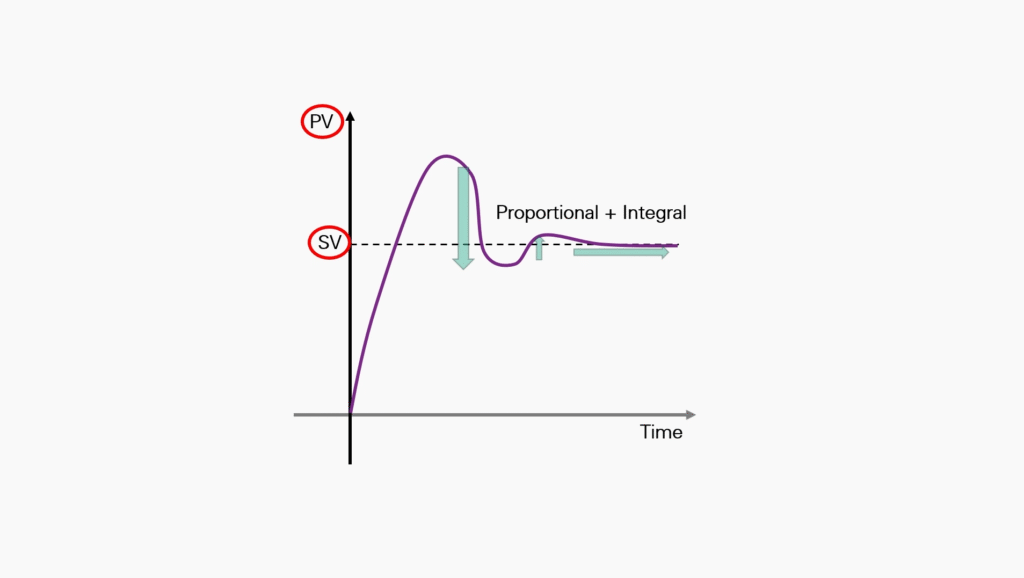
Using Proportional and Integral together will result in less oscillation when headed towards the set value.
Derivative
This predicts any future values in the “error”, based on its current rate of change.
By adding Derivative control, quick corrective action can be obtained at the beginning of the condition, but if it’s set too long, oscillations can occur and the control loop can become unstable.
In order to use Derivative time, the Process Variable must be a very clean signal.
Set Value
This can also be called the target value or set point.
This is the value you want to reach.
Once the Proportional, Integral and Derivative controls are adjusted properly, this is the overall value to meet.
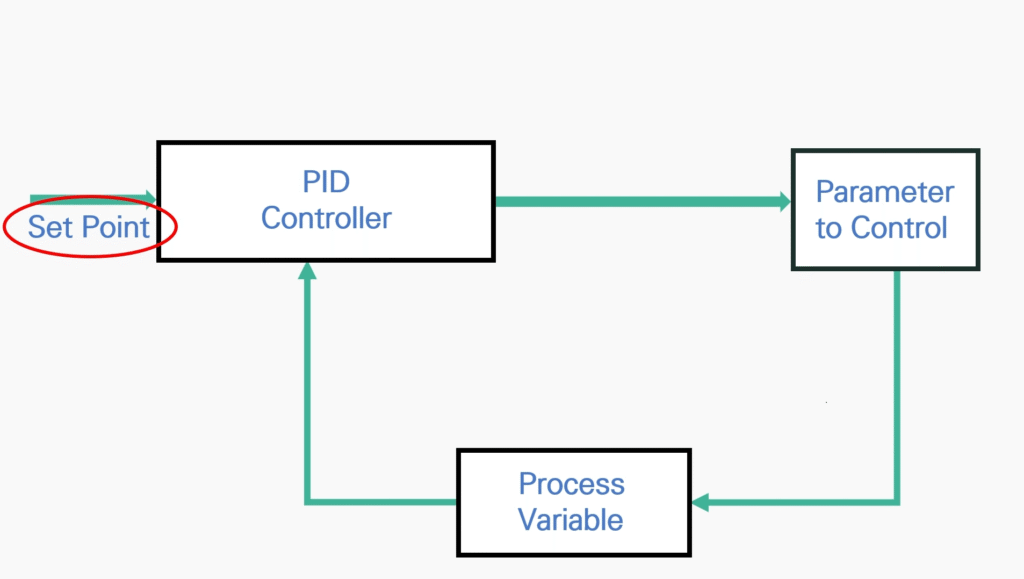
Control Variable
The Control Variable or the Parameter to Control. This would be the device (ex. heater or oven) that is being controlled by the process variable.
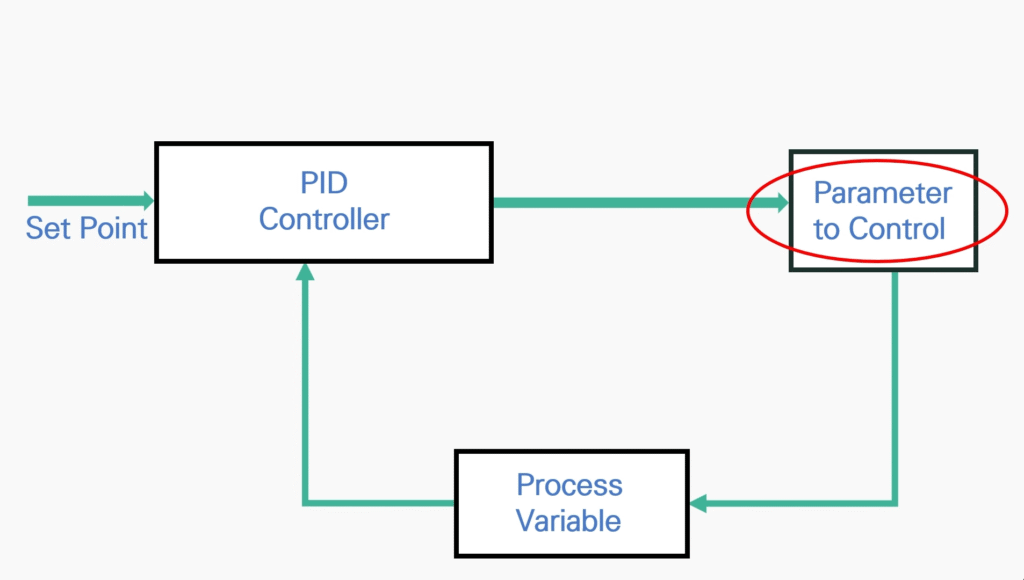
Process Variable
The Process Variable or Process Value is the sensor or meter, whichever you are using to get the current measurement of the control variable (ex. Oven or Heater).
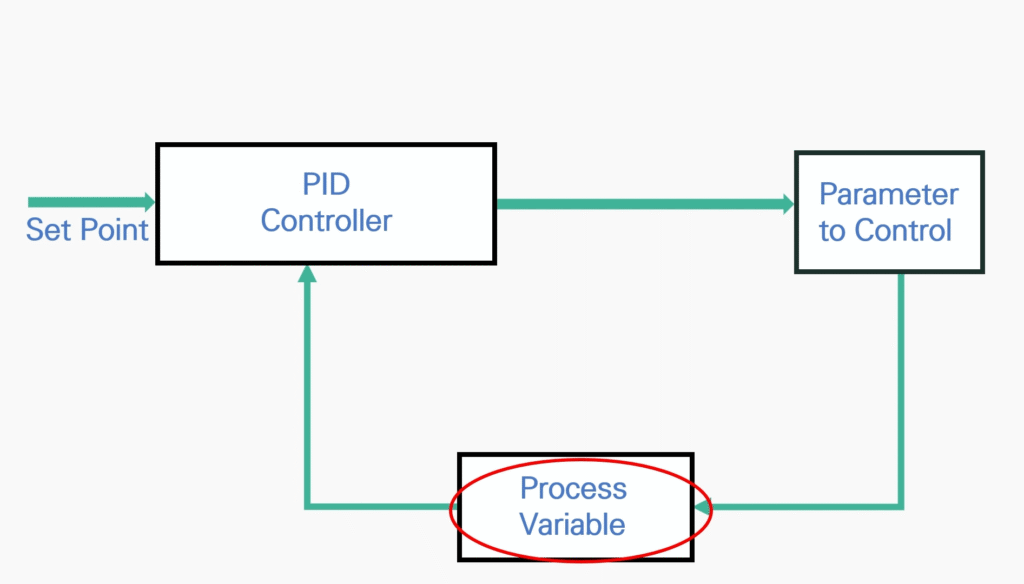
Sometimes the result of the PID Calculation is called the Manipulative Value or MV.
Cruise Control Example
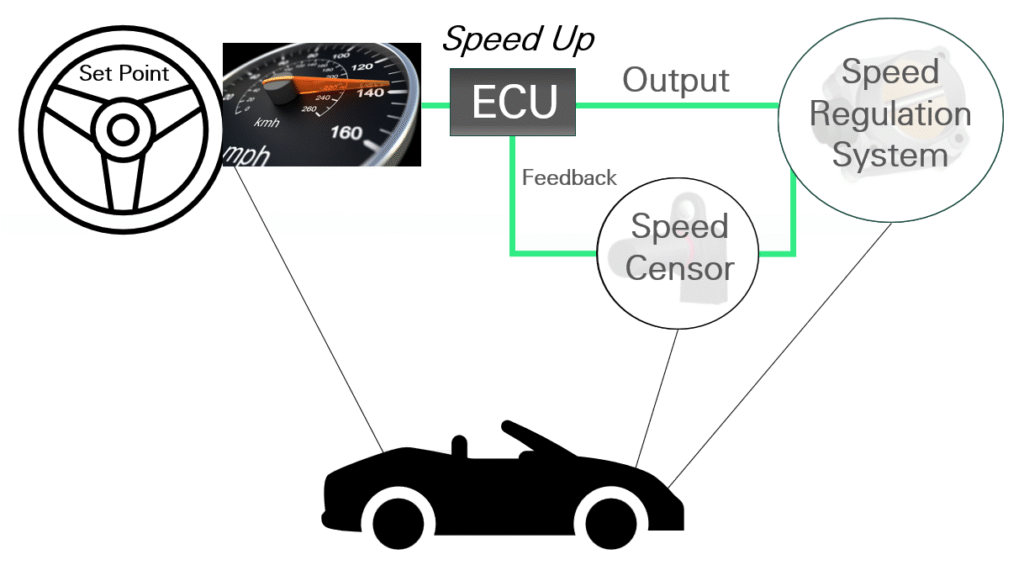
The Cruise Control in your car can be an example of a PID Loop.
- First, get your vehicle to the desired speed.
- Then set the cruise control which is the set value or target value.
- The cruise control then sends output signals to the throttle to regulate the speed. This is the control variable.
- A speed sensor provides the control loop feedback to tell the cruise control if the car should speed up or slow down. This is the process value or process variable.
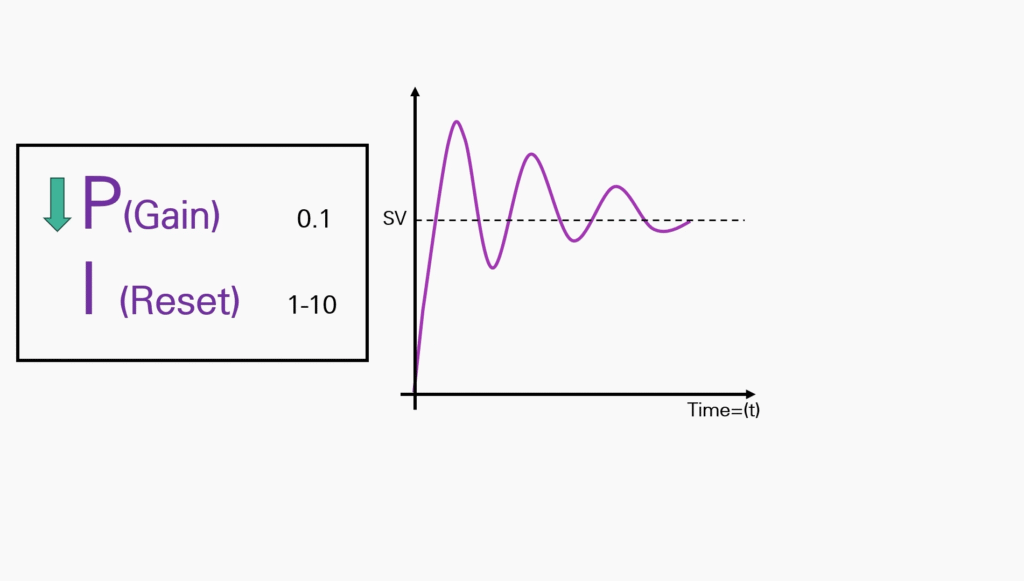
Proportional Gain + Integral Control
For example: If your Process Variable changed quickly, you’ll start with a low gain possibly as low as 0.1 while your Integral (Reset) is adjusted between 1 and 10 repeats per minute.
Conversely, if the process variable changed slowly, start with a higher gain and lower reset.
For example, the Proportional Gain would be between 2 and 8, and the Integral would be between 0.05 and 0.5.
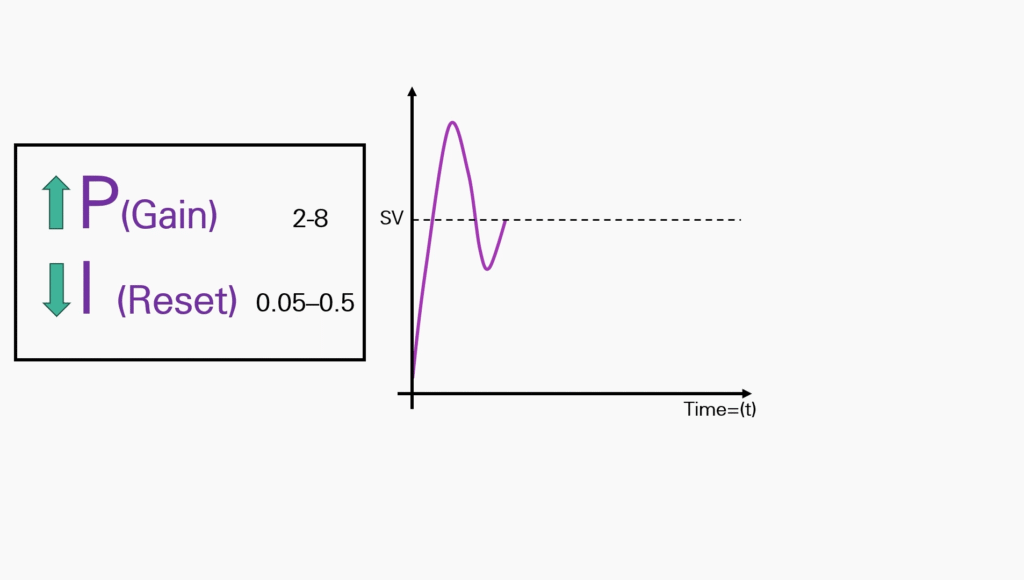
Continue this pattern until a stable process is achieved.
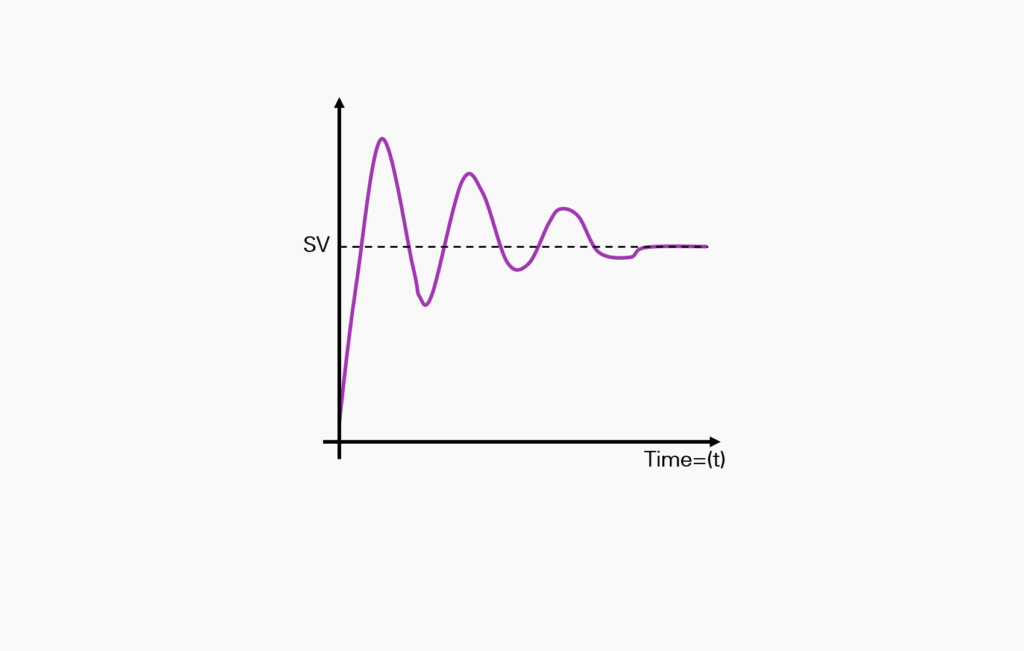
PID Measured Approach
A measured approach is starting with a low gain with Integral and Derivative disabled.
Incrementally adjust the gain by doubling the value, which in turn will oscillate the process.
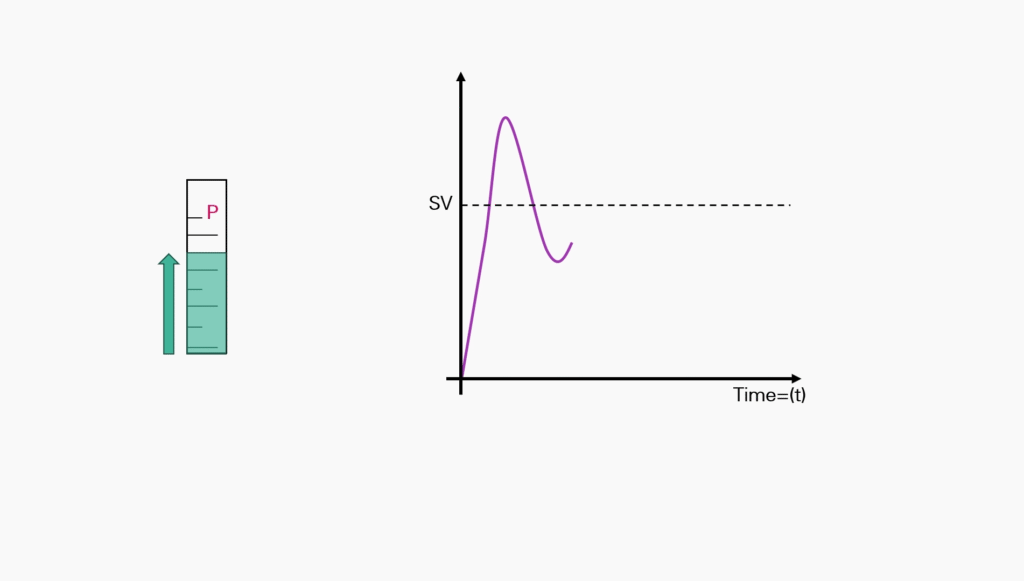
Adjust the gain value down by 50 percent.
Then apply a small amount of integral value and monitor the process.
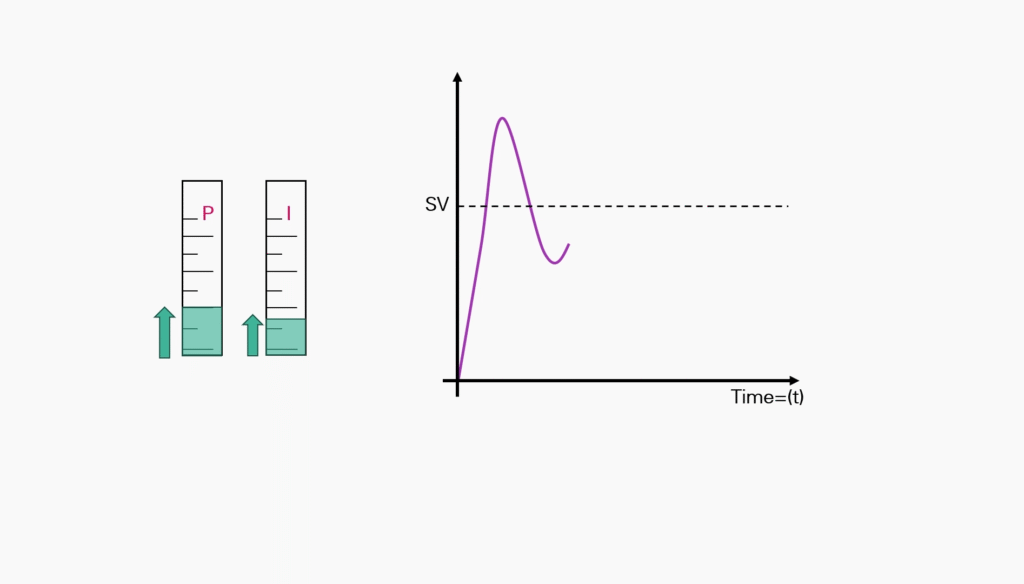
Double the Integral Value incrementally until small amounts of oscillations occur.
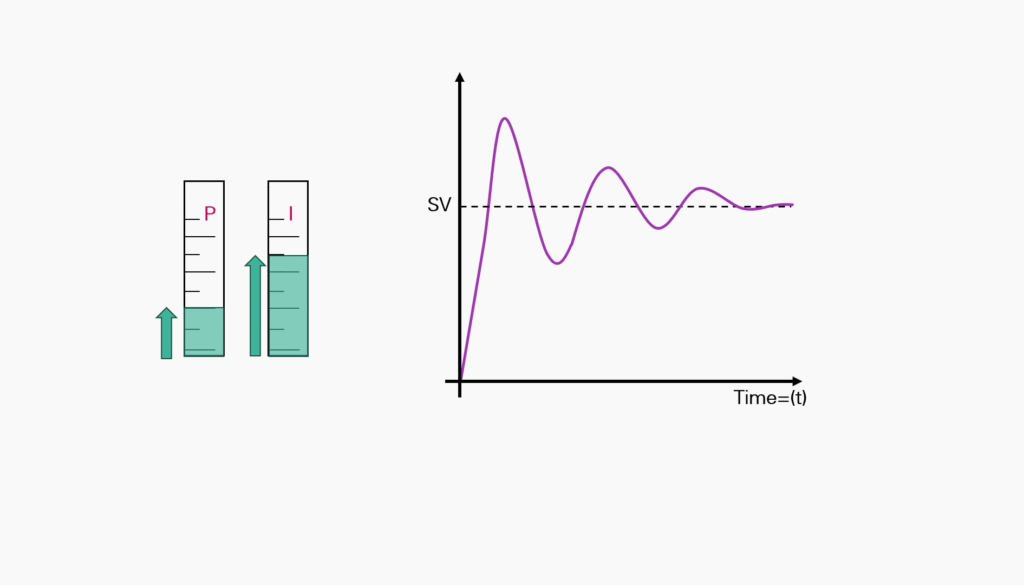
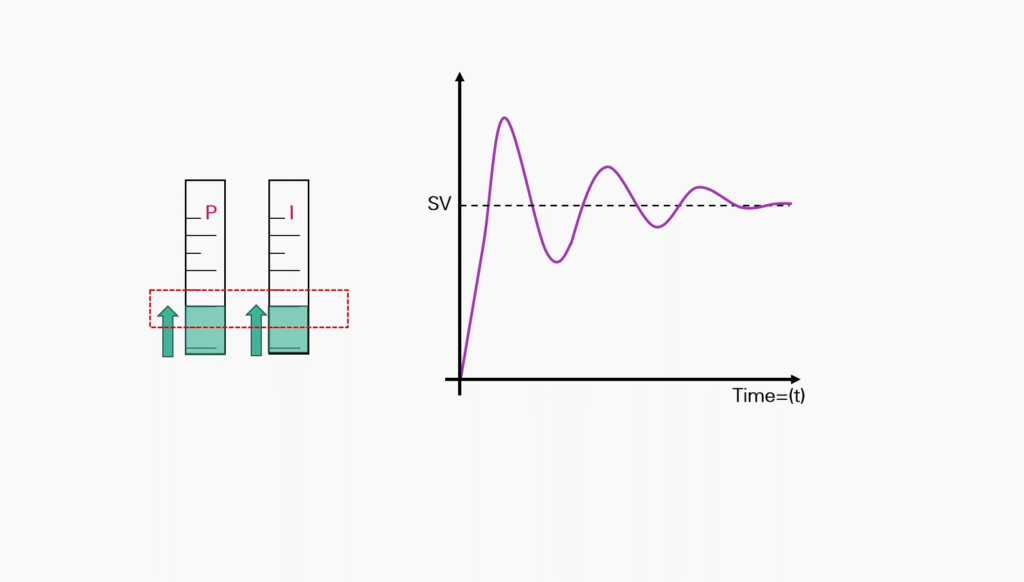
Lower the Integral value by 50 percent.
After this you should be close to the set value (target value).
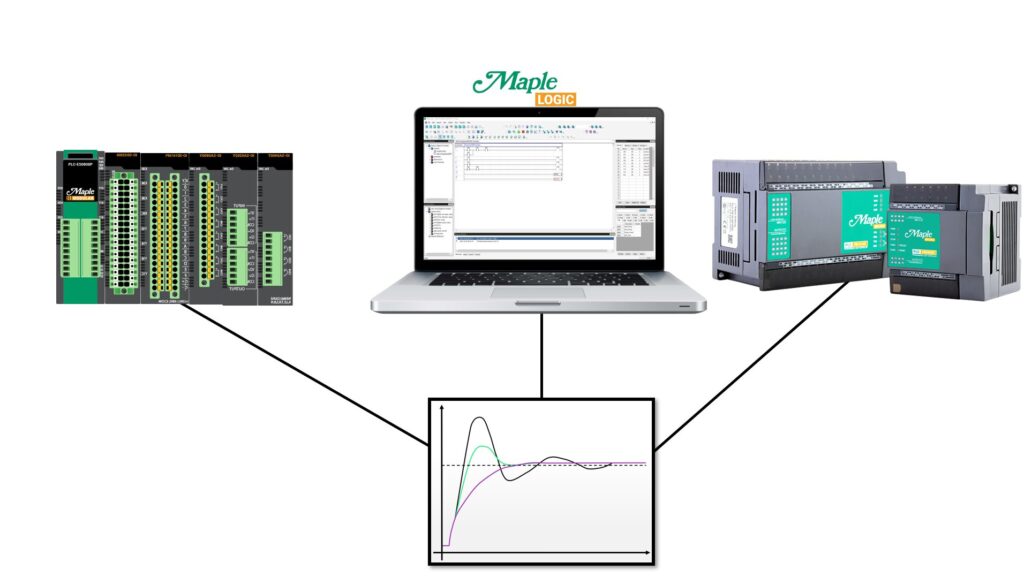
You can use a PID with the Maple PLC’s (Modular or Micro), while utilizing the PLC control software MapleLogic. (Expansion modules only available with Maple Modular PLC)
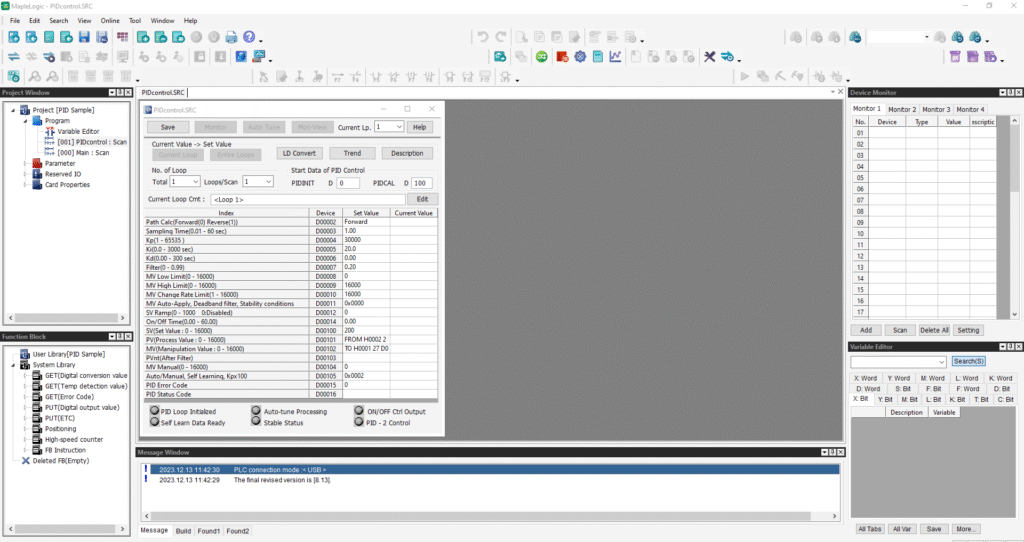
You can configure a PID and connect to a Maple PLC using the Control Software MapleLogic.
Resources & Documentation
Maple PLC/MapleLogic Resources
More
Tutorials
Sample Projects
See our Support Center for a complete list of Quick Start and Installation Guides
About the Author
